SiLU(Swish)란
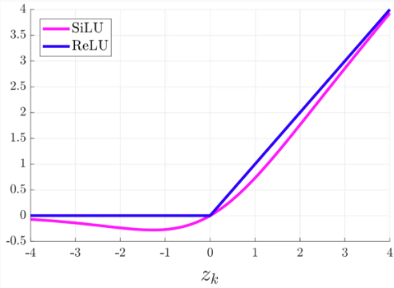

sigmoid에 입력값을 한 번 더 곱해주는 모양이다.
연구에서 활성화 함수를 ReLU로 사용한 모델에서 단순히 SiLU로 바꾼 실험에서 SiLU가 ReLU를 압도한다고 한다.
그 이유는 정확하진 않지만 아래 4가지로 추측하고 있다.
- Unbounded above where x≥0
- Bounded below where x<0
- Non monotonicity
- Smooth figure
1. Unbounded above where x≥0
SiLU의 범위가 ReLU의 범위와 마찬가지로 [0,∞)이다. 이는 gradient vanish를 막아준다.
2. Bounded below where x<0
너무 큰 음수값을 0으로 보내는 특성이다.
ReLU에서는 음수값에 대해서 무조건 0을 보내기 때문에 dying ReLU에 직면한다.
따라서 Leaky ReLU나 PReLU가 파생형으로 나왔는데 SiLU는 어느 정도 작은 음수값에 대해서 허용하고 너무 큰 음수값은 0으로 보낸다.
어느 정도 작은 음수값에 대해 허용하는 특성은 Non monotonicity 특성과도 이어진다.
3. Non monotonicity
SiLU는 약간의 음수를 허용하고 양수 부분은 직선 그래프가 아니다.
ReLU와 비슷하게 생겼지만 표현력이 좋다고 한다.
따라서 gradient가 작은 음수로 전해져도 온전히 이전 layer로 전할 수 있어서 학습이 잘 된다.
4. Smooth figure
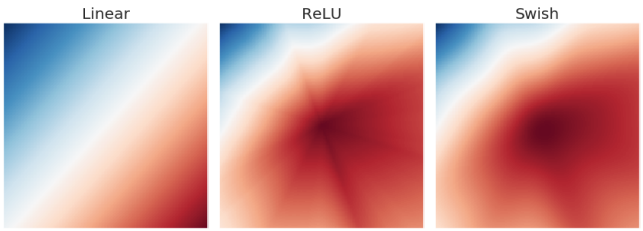
위 그림은 6개의 layer를 가진 임의의 신경망을 학습해 출력 layer의 activation map이다.
ReLU에서 별모양은 activation map 상에서 갑작스러운 변화를 의미한다.
이는 작은 변화에도 민감하게 반응해 학습을 어렵게 하는 원인이라고 한다.
SiLU(Swish)처럼 경계가 흐릿하면 ReLU와는 반대로 작은 변화에는 작게, 큰 변화에는 크게 반응하여 원활하게 학습할 수 있다.
'AI' 카테고리의 다른 글
| Hailo Data Compiler 사용 (0) | 2025.12.18 |
|---|---|
| Hailo 관련 SW 설치 (2) | 2025.12.18 |
| [YOLO] COCO 데이터 형식에서 YOLO 데이터 형식으로 바꾸기 (0) | 2025.02.11 |
| [YOLOv8] custom training하여 바닥 Instance Segmentation하기 (0) | 2025.02.10 |
| [YOLOv7] custom training (2) | 2023.01.13 |